上次说到了Vigenere加密以及解密的算法,但是如何破译这样的密码,也是很有意思的,这篇博客就是实现一个这样的破译,主要针对的是通过Vigenere加密的密文,那么就开始吧~
任务要求:
原理介绍:
按照我们之前的说法,我们先介绍一下Caesar加密的缺点。对于一个稍微有点点密码学功底的人来说,Caesar密码的安全强度几乎为零,正如我们是上篇博客所讲的Caesar加密,加密的密钥充其量也就24个,也就是说,不管移动多少个字符,最多进行24次猜解就可以破译出来。
当然,这只是一种解密方法,也是比较笨的一种方法,而且这种方法并不适用于我们的Vigenere密码破解,因为我们没办法列举出所有的情况。
这里我们介绍破解Caesar密码的另一类方法,称为(字母)频度分析法。
假设大家都知道,英语中的字母出现概率是有差别的,其实对于一种特定的自然语言,如果文本足够长,那么各个字母出现的概率就是相对稳定的,具体的概率统计如下图所示:
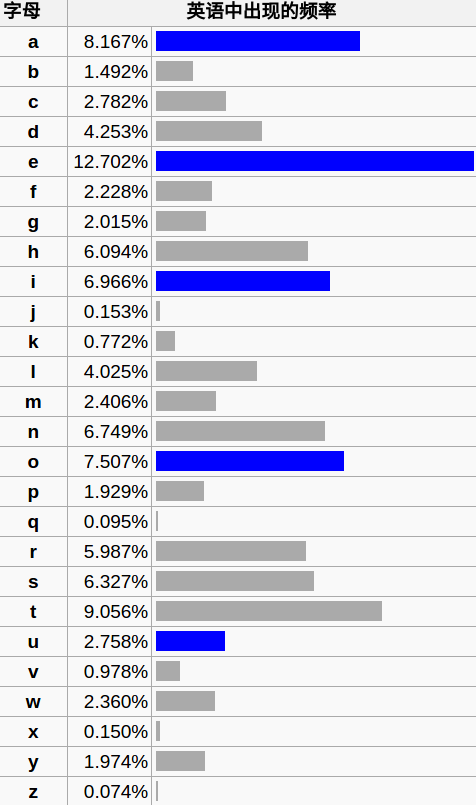
这样我们根据以上的频度表,以及根据我们的Caesar密文中的统计出来的各个词的拼读,对应一下就可以找到密文对应的明文,再然后对应密文与明文就可以找到相应的加密的密钥。很简单吧,其实能想到这个想法并不简单的。
由上一篇的博客介绍,你应该知道了Vigenere密码分解之后其实就是多个Caesar密码。所以我们如果知道密钥的长度,每隔这个长度将原来的Vigenere密文分解为多个Caesar密文,再做上述的工作,是不是就完成了我们的破译工作?思路就是这样,但是怎么确定我们的密钥长度?那么我们接下来就讲讲怎么解决这个问题吧。
确定密钥长度
这个在网上搜集到的资料其实是有两种方法的。分别称为Kasiski测试法和Friedman测试法,但是本文给到的代码是基于第二个方法的,不过在此之前,我们还是先讲讲这两个方法的思路吧。
Kasiski测试法
Kasiski测试法是由Friedrich Kasiski于1863年给出了其描述,然而早在约1854年这一方法就由Charles Babbage首先发现。
它的思想是基于这样的一个事实:两个相同的明文段加密成相同的密文段,它们之间的距离为Length,那么密钥的长度就是距离Length的约数。
而当密文的长度很长时,我们便可以多找几组这样拥有重复密文段,找出他们间距的相同约数就是密钥的长度。
关于这个方法的代码,本文并未涉及,大家有兴趣可自行查阅资料实现。
另:机智的你也许发现了,我们这种方法其实并没有涉及到我们刚才说的统计频度,所以我们的重点不是这个方法,接下来就是本文的重点了。
Friedman测试法
首先我们讲一个概念:重合指数(IC,index of coincidence)。百度一下这个概念的话,搜到的结果可能不是令人很满意,我也是找了很多资料,感觉如下的概念说的很清楚,分享给大家。
重合指数表示:两个随机选出的字母是相同的概率,对于我们的英文字母来说,即以上概率即为随机选出两个A的概率+随机选出两个B的概率+….+随机选出两个Z的概率。
前人也为我们统计出了这个数字,为0.65。
即 P(A)^2 + P(B)^2 + P(C)^2 + … + P(Z)^2 = 0.65.
而利用这一概念推测密钥长度的原理为:对于一个Caesar密码的序列,由于所有字母的位移程度是一样的,所以密文的重合指数等于原文的重合指数。
将这一概念迁移到我们的Vigenere密文上,我们只要计算不同密钥长度下的重合指数,只要重合指数接近期望的0.65时,我们便可以推测当前的长度就是我们的密钥长度。
举个例子:
密文为:AAABBCCDDDDEEEFG
首先我们测试密钥长度=1,首先统计上述密文中每个字母出现的次数(A-Z):
A:3 B:2 C:2 D:4 E:3 F:1 G:1 H:0 … Z:0
然后我们根据上述公式计算重合指数P,如果 P != 0.65,我们就尝试密钥长度2。
假设为2的话,将上述的密文分成两组:
组1:A A B C D D E F
组2:A B C D D E E G
再分别计算重合指数,如果这两个的重合指数都接近于0.65,那么我们就可以基本确定密钥的长度为2了。如果不是,那么继续往下分。
理论上来说,我们得到的密文长度越长,通过这个方法分析得到的效果会更好,实际上在我测试的结果中,也确实符合刚才的说法。
实现
Friedman测试法确定密钥长度
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
| // Friedman测试法确定密钥长度
public int Friedman(String ciphertext) {
int keyLength = 1; // 猜测密钥长度
double[] IC; // 重合指数
double average; // 平均重合指数
ArrayList<String> cipherGroup; // 密文分组
while (true) {
IC = new double[keyLength];
cipherGroup = new ArrayList<String>();
average = 0;
// 1 先根据密钥长度分组
for (int i = 0; i < keyLength; ++i) {
StringBuffer temporaryGroup = new StringBuffer();
for (int j = 0; i + j * keyLength < ciphertext.length(); ++j) {
temporaryGroup.append(ciphertext.charAt(i + j * keyLength));
}
cipherGroup.add(temporaryGroup.toString());
}
// 2 再计算每一组的重合指数
for (int i = 0; i < keyLength; ++i) {
String subCipher = new String(cipherGroup.get(i)); // 子串
HashMap<Character, Integer> occurrenceNumber = new HashMap<Character, Integer>(); // 字母及其出现的次数
// 2.1 初始化字母及其次数键值对
for (int h = 0; h < 26; ++h) {
occurrenceNumber.put((char) (h + 65), 0);
}
// 2.2 统计每个字母出现的次数
for (int j = 0; j < subCipher.length(); ++j) {
occurrenceNumber.put(subCipher.charAt(j), occurrenceNumber.get(subCipher.charAt(j)) + 1);
}
// 2.3 计算重合指数
double denominator = Math.pow((double) subCipher.length(), 2);
for (int k = 0; k < 26; ++k) {
double o = (double) occurrenceNumber.get((char) (k + 65));
IC[i] += o * (o - 1);
}
IC[i] /= denominator;
}
// 3 判断退出条件,重合指数的平均值是否大于0.065
for (int i = 0; i < keyLength; ++i) {
average += IC[i];
}
average /= (double) keyLength;
if (average >= 0.06) {
break;
} else {
keyLength++;
}
} // while--end
return keyLength;
}// Friedman--end
|
破译密文
这里给出来的是打印出来了具体的密钥和明文,实际上可以直接写一个类,类中设计两个属性值,一个密钥属性,一个明文属性,直接赋值下就可以了。相信机智的你可以完成这个操作。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
| public void decryptCipher(int keyLength, String ciphertext) {
int[] key = new int[keyLength];
ArrayList<String> cipherGroup = new ArrayList<String>();
double[] probability = new double[] { 0.082, 0.015, 0.028, 0.043, 0.127, 0.022, 0.02, 0.061, 0.07, 0.002, 0.008,
0.04, 0.024, 0.067, 0.075, 0.019, 0.001, 0.06, 0.063, 0.091, 0.028, 0.01, 0.023, 0.001, 0.02, 0.001 };
// 1 先根据密钥长度分组
for (int i = 0; i < keyLength; ++i) {
StringBuffer temporaryGroup = new StringBuffer();
for (int j = 0; i + j * keyLength < ciphertext.length(); ++j) {
temporaryGroup.append(ciphertext.charAt(i + j * keyLength));
}
cipherGroup.add(temporaryGroup.toString());
}
// 2 确定密钥
for (int i = 0; i < keyLength; ++i) {
double MG; // 重合指数
int flag; // 移动位置
int g = 0; // 密文移动g个位置
HashMap<Character, Integer> occurrenceNumber; // 字母出现次数
String subCipher; // 子串
while (true) {
MG = 0;
flag = 65 + g;
subCipher = new String(cipherGroup.get(i));
occurrenceNumber = new HashMap<Character, Integer>();
// 1.1 初始化字母及其次数
for (int h = 0; h < 26; ++h) {
occurrenceNumber.put((char) (h + 65), 0);
}
// 1.2 统计字母出现次数
for (int j = 0; j < subCipher.length(); ++j) {
occurrenceNumber.put(subCipher.charAt(j), occurrenceNumber.get(subCipher.charAt(j)) + 1);
}
// 1.3 计算重合指数
for (int k = 0; k < 26; ++k, ++flag) {
double p = probability[k];
flag = (flag == 91) ? 65 : flag;
double f = (double) occurrenceNumber.get((char) flag) / subCipher.length();
MG += p * f;
}
// 1.4 判断退出条件
if (MG >= 0.055) {
key[i] = g;
break;
} else {
++g;
}
} // while--end
} // for--end
// 3 打印密钥
StringBuffer keyString = new StringBuffer();
for (int i = 0; i < keyLength; ++i) {
keyString.append((char) (key[i] + 65));
}
System.out.println("\n密钥为: " + keyString.toString());
// 4 解密
StringBuffer plainBuffer = new StringBuffer();
for (int i = 0; i < ciphertext.length(); ++i) {
int keyFlag = i % keyLength;
int change = (int) ciphertext.charAt(i) - 65 - key[keyFlag];
char plainLetter = (char) ((change < 0 ? (change + 26) : change) + 65);
plainBuffer.append(plainLetter);
}
System.out.println("\n明文为:\n" + plainBuffer.toString().toLowerCase());
}
|
参考资料:
维吉尼亚密码及其破解
【密码学】维吉尼亚密码加解密原理及其破解算法Java实现
以上是本次博客的全部内容,感谢驻足~
